
Reference Publication: Fairey, P., J. Tait, D. Goldstein, D. Tracey, M. Holtz, and R. Judkoff, "The HERS Rating Method and the Derivation of the Normalized Modified Loads Method." Research Report No. FSEC-RR-54-00, Florida Solar Energy Center, Cocoa, FL, October 11, 2000. Disclaimer: The views and opinions expressed in this article are solely those of the authors and are not intended to represent the views and opinions of the Florida Solar Energy Center. |
The
HERS Rating Method and the Derivation
of the Normalized Modified Loads
Method
Philip
Fairey†
Jim Tait‡
Florida
Solar Energy Center (FSEC)
David
Goldstein
Natural Resources Defense Council
Dick Tracey¥
Consultant
Michael Holtz†
Architectural Energy Corporation
Ron Judkoff†
National Renewable Energy Laboratory
†Member, National HERS Council
Technical Committee
‡ Chairman,
NASEO Buildings Committee
¥Vice Chairman,
National HERS Council Technical Committee
FSEC-RR-54-00
ABSTRACT
This paper provides much of the historical background surrounding the contentious development of a national, uniform rating method for rating the energy-efficiency of homes. A full derivation of the most recently adopted rating method, the Normalized Modified Loads Method, is provided in detail and the issues and events leading up to the development of each of the succeeding methods are described.
Ever since the inclusion of Home Energy Rating Systems in the 1992 Energy Policy Act, the most contentious issue associated with them has been the development of a uniform rating method. To date, four succeeding methods have been proposed: 1) the "Original" Method, 2) the Equipment Adjustment Factor Method, 3) the Modified Loads Method, and 4) the Normalized Modified Loads Method. Since the beginning, the process of reaching a national consensus on an acceptable rating method has been plagued by the competing market interests of the electric and gas industry. The effort to find a solution that is equitable and "fuel neutral" has proven to be a quest not unlike that for the holy grail.
The national discussion that has ensued from this effort has worked to clarify, and in some cases resolve, many of the issues involving the building energy efficiency marketplace, national building codes and appliance standards, and energy and environmental policy. It has led to a fuller appreciation of the complexity of building energy efficiency, its varied definitions and meanings, and to the adoption for the first time by a national association of governmental officials, a set of uniform technical guidelines for rating the energy efficiency of homes.
The Succession of Methods
In 1993, in response to the 1992 Energy Policy Act, the US Department of Energy (DOE) contracted with the newly established HERS Council to develop a uniform Home Energy Rating System. Since that time, the most contentious issue associated with home energy rating systems has been the development of a uniform rating method. To date, four succeeding rating methods have been proposed, as follows: 1) the "Original" Method, 2) the Equipment Adjustment Factor Method, 3) the Modified Loads Method, and 4) the Normalized Modified Loads Method.1
The "Original" Method of rating home energy efficiency was developed by the HERS Council Technical Committee and published almost simultaneously in July 1995 by the HERS Council2 and by the U.S. Department of Energy (DOE) in a Notice of Proposed Rule (NOPR).3 This rating method was developed within the framework of a set of guiding principles approved by the HERS Council's Board of Directors, which included the following:
-
The method should be based on reference standards that do not change over time so that the point score of a home can not inflate or deflate with time.
-
The method should be consistent with the 1993 version of the Council of American Building Officials (CABO) Model Energy Code (MEC) so as to comply with the 1992 Energy Policy Act (EPAct ´92).
-
The method should be constructed using a 100 point scale with higher points indicating greater efficiency, such that a score of 80 indicates compliance with the 1993 MEC and a score of 100 indicates purchased energy consumption of zero.
-
The method should be fuel neutral and provide no market incentives for fuel switching so as to comply with the spirit and intent of EPAct ´92.
Each of the methods developed to succeed the "original" rating method have been developed in an effort to achieve the elusive and very contentious "fuel neutrality" ideal that is embodied in this final objective.
The "Original" Method
Shortly after its publication by the HERS Council and DOE in July 1995, a significant flaw was discovered in the "original" method. That flaw stems from the equation used to calculated the point score, which is as follows:
| Point score = 100 - 20 * (ER / EC) | Eq. 1 |
|||
| where: | ||||
| ER = | Total estimated purchased energy consumption for heating, cooling and hot water for the Rated Home. | |||
| EC = | Total estimated purchased energy consumption for heating , cooling and hot water for the Reference Home. | |||
The framers of this method believed that fuel neutrality was provided by the Reference Home requirements, whereby the fuel types were required to be the same as the fuel types of the Rated Home. At the time, it was believed that this simple solution would result in fuel neutrality because competing fuel types would never be compared against each other in the calculation of the point score.
Upon closer examination, however, a flaw was discovered. The root of the flaw lay in the fact that EC, the Reference Home energy consumption, is a "floating" reference, the value of which changes as a function of the fuel type selected. As a result, the point score of a home could be manipulated significantly by "switching" fuel types in the Rated Home. Furthermore, this occurs at every place on the point scale except for the case where the Rated Home energy consumption equals the Reference Home energy consumption (i.e. a point score of exactly 80).
Much contention resulted from this flaw in the form of the ongoing "fuel wars" between the electric and gas industries. However, it is important to point out that this flaw is mathematical in nature it occurs no matter whether energy is counted by site use, source use or cost.
The key to the failure is in the "rating fraction" term (EC / ER) of Eq. 1. Table A below provides a vivid example that examines the point score of a home with energy efficient envelope features and minimum standard equipment. When the hot water heater is changed from the electric minimum standard to the natural gas minimum standard, the point score, as calculated by Eq. 1, decreases by 0.8 points, which is supposed to represent a 4% reduction in the potential energy-efficiency of the home. In the example, both the numerator (EC) and the denominator (ER) of the rating fraction change by the same amount (14.31) between the two homes. This change, especially with respect to the denominator, is the key to the flaw in the method. All methods that use energy consumption or energy cost for the rating fraction and require the fuel type to be the same in the Rated and Reference Homes will experience this mathematical flaw.
Table A. Comparison of the calculated
point scores for a home in which the hot
water heater fuel type is switched between electric and natural gas.
Rated Home |
Reference Home |
|||||
| With electric hot water: | Load |
Eq.Eff. |
Energy |
Load |
Eq.Eff. |
Energy |
Heating |
25 |
2.0 |
12.50 |
40 |
2.0 |
20.00 |
Cooling |
20 |
3.413 |
5.86 |
30 |
3.413 |
8.79 |
Hot Water |
20 |
0.88 |
22.73 |
20 |
0.88 |
22.73 |
Total energy use |
41.09 |
51.52 |
||||
Point Score |
84.0 (by Eq.
1) |
|||||
| With gas hot water: | Load |
Eq.Eff. |
Energy |
Load |
Eq.Eff. |
Energy |
Heating |
25 |
2.0 |
12.50 |
40 |
2.0 |
20.00 |
Cooling |
20 |
3.413 |
5.86 |
30 |
3.413 |
8.79 |
Hot water |
20 |
0.54 |
37.04 |
20 |
0.54 |
37.04 |
Total energy use |
55.40 |
65.83 |
||||
Point Score |
83.2 (by
Eq. 1) |
|||||
A simple mathematical exercise can be used to illustrate the problem shown in Table A. Take any fraction that evaluates to a value different than unity (e.g. use 3/4) then add any value to both the numerator and denominator of that fraction (e.g. add 1 to each giving 4/5). Resolve the fraction and you will find that its value has changed (e.g. from 0.75 to 0.80).
Thus, if the denominator of the rating fraction used in the point score equation is allowed to change as a function of fuel type, then the method will fail the fuel neutrality test by virtue of the fact that the reference (the denominator) is floating. When this occurs, each home will have multiple standards against which it may be judged (scored) and the system will certainly be "gamed" to the advantage of one fuel type or another.
The Equipment Adjustment Factor Method
In December 1995, a Joint Technical Committee of the National Association of State Energy Officials (NASEO) and the Residential Energy Services Network (RESNET) met in Scottsdale, Arizona at the annual Department of Energy's All States Conference to seek a solution to this issue. A rating method named the Equipment Adjustment Factor Method was proposed and adopted by the members of this committee. The following month, January 1996, the NASEO/RESNET Joint Technical Committee met with the HERS Council Technical Committee in Washington, DC, where the Equipment Adjustment Factor Method was adopted by the consensus.
The Equipment Adjustment Factor Method was seriously studied by the HERS Council Technical Committee over the next few months and an analysis was conducted comparing it with the original method.4 It solved the "floating" denominator problem by adjusting the energy consumption values for equipment other than electric by the ratio of the NAECA minimum standard for that fuel type with respect to the minimum standard for the equivalent electric equipment. For example, the natural gas space heating Equipment Adjustment Factor would be 0.78 / 1.99 = 0.39 (the efficiency of the minimum standard gas equipment [AFUE = 0.78] divided by the minimum standard electric equipment efficiency [HSPF = 6.8 divided by the Btu/watt conversion factor of 3.413]). This has the effect of forcing the Reference Home to contain the minimum standard electric heating equipment, and if the Rated home contains gas heating equipment, then its estimated energy consumption for heating is multiplied by 0.39, thereby forcing a comparison in the rating fraction that is equivalent to an electric-to-electric comparison. In this manner, the rating fraction's denominator remains consistent regardless of the fuel type used in the Rated Home and all fuel types other than electric are converted to their electric "equivalents" through a table of adjustment factors. This method, however, still relied on estimated site energy use values for its rating fraction. This left one remaining issue, as follows:
Rating directly by energy consumption misrepresents the relative value of envelope efficiency measures with respect to equipment efficiency measures.
Since heating, cooling and hot water equipment generally have significantly different efficiencies it is easy for the most cost effective improvements to be misrepresented or "hidden" by this method. For example, in a cooling dominated climate rating by direct energy consumption may often give the "signal" that winter envelope performance has greater importance than summer envelope performance of course, the opposite is likely true. This occurs because the winter heating load is divided by roughly 2 to give its energy use while the summer cooling load is divided by roughly 3 to give its energy use. Thus, for minimum standard equipment, the envelope features that impact the cooling load will be given only 2/3 as much "weight" as the envelope features that impact the heating load.
In April 1996, based on comments received on its first NOPR, DOE published the Equipment Adjustment Factor Method as the proposed rating method in a commentary on its original NOPR.5 Nonetheless, the HERS Council Technical Committee continued to work on a simpler, more straight-forward alternative called the Modified Loads Method. In June 1996 it recommended this method to the HERS Council Board of Directors, which adopted it, and in August 1996, the HERS Council published Version 2 of their HERS Technical Guidelines.6 This version of the Guidelines replaced the "Original" rating method with the Modified Loads Method.
During the summer and fall of 1996, before the House Energy and Water Appropriations Sub Committee, the American Gas Association (AGA) was able to successfully convince congress that the rating method proposed by DOE grossly misrepresented the interests of the natural gas industry. As a result, DOE's funding for Home Energy Rating System activities was severely curtailed and DOE's proposed Rule on Voluntary Home Energy Rating Guidelines was never published. It has been reported, however, that if DOE had promulgated its final home energy rating Rule, it would have contained the Modified Loads Method rather than the Equipment Adjustment Factor Method of rating.7
The Modified Loads Method
The Modified Loads Method for rating the energy-efficiency of homes is specifically designed to avoid the problems encountered with the "Original" and the Equipment Adjustment Factor Methods. The results of the study conducted by the HERS Council on the matter (see footnote 4) are summarized in Figure 1 below.
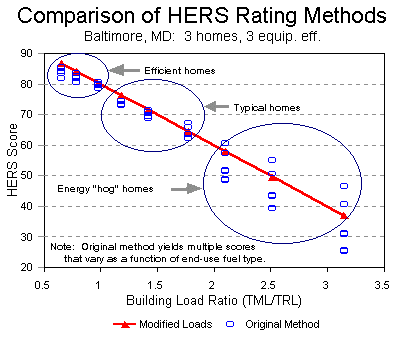
Figure 1. Comparison of the "Original" and
the Modified Loads
Methods of rating the efficiency of homes
The Modified Loads Method emerged as the superior method from a series of proposed alternatives that were considered in detail by a NASEO/RESNET Joint Technical Committee and the HERS Council Technical Committee. It was adopted by the HERS Council Board of Directors and published as the "Rating Method" in Version 2 of their HERS Technical Guidelines and was in widespread use within the HERS industry, the DOE Build America program and the EPA ENERGY STAR® New Homes program from 1996 through 1999.
The underlying principle of the Modified Loads Method and the solution to the problems encountered with previous methods turns out to be quite simple do not use energy consumption to construct the rating fraction, use the building loads instead. Since the loads on building end uses do not change as a function of fuel type, the denominator of the rating fraction (the sum of the Reference Home loads) remains the same across all fuel types! Modify the loads of the Rated Home where necessary to account for any changes in equipment efficiency that occur when the Rated Home's equipment efficiencies are different from the Reference Home equipment efficiency standards. Then use the Rated Home's "modified" loads and the Reference Home's actual loads to construct the rating fraction. This solves both the "floating" denominator problem and the equipment vs. envelope efficiency problem because building loads, rather than energy consumption are used to construct the rating fraction.
It is important to point out that, in addition to solving the "floating" denominator
and envelope vs. equipment efficiency problems, this approach also renders
the "site vs. source vs. cost" argument irrelevant it
does not matter which way energy consumption is counted, the point score
will be identical no matter whether you count by site energy consumption,
source energy consumption or cost.
To illustrate how the method is structured and how it successfully
provides a stable point score, it is necessary to first carefully define
two terms.
Load is defined as the quantity of heat that must be added to or removed from the building (or the hot water tank) to satisfy specific levels of service in other words, to keep the space temperature at a specified thermostat setting or to supply a given quantity of hot water at a given temperature.
Energy Use is defined as the quantity of electricity, gas or other fuel required by the equipment that satisfies the load.
It is quite important to understand the difference between these two terms. Loads do not use energy, rather they cause energy use. Energy is only used by equipment, and each different piece of equipment has a specific efficiency rating with which it can satisfy a given load. This concept is expressed in equation form as follows:
Load |
||
Energy Use = |
------------------------------ |
Eq. 2 |
Equipment Efficiency
Rating |
The main premise of the Modified Loads Method arises directly from
the above mathematical expression, and can be stated as follows:
Doubling the efficiency rating of a piece of equipment is equivalent to dividing the load on that piece of equipment by 2.
Thus, for a given building with known loads, the loads can be modified
in such a way as to accurately account for the impact of changes in
equipment efficiency.
Heating and Cooling loads for buildings are determined from the building
envelope thermal characteristics and local climate data, and hot water
loads are determined from the number of bedrooms (as a surrogate for
occupants) and local climate data (as the determinate of tank inlet
water temperature). Rating systems are constructed such that two sets
of such data are computed one set for the Reference Home (which
is a geometric twin of the actual home with its thermal performance
characteristics specified to minimally comply with MEC ´93) and
one set for the Rated Home with its thermal performance characteristics
specified as those of the actual home being rated. Thus, the thermal
performance characteristics of the Rated Home envelope can be directly
compared with the minimum national standards by comparing these two
load computations.
In addition to standards for envelope thermal characteristics, national minimum standards established as a result of the National Appliance Energy Conservation Act (NAECA) exist for equipment efficiency. These NAECA minimums are used as the reference standard for equipment efficiency in the Modified Loads Method.
Consistent with the premise of equivalence between equipment efficiency and load, it is possible to use these two sets of national minimum standards (MEC for the envelope and NAECA for the equipment) to "score" the overall energy-efficiency potential of a home with respect to both its envelope components and its equipment.
First, the heating, cooling and hot water loads for the two homes (Reference and Rated) are computed. Next, a ratio is taken between the NAECA minimum standard equipment efficiency (the Reference used as the numerator) and the efficiency of the equipment to be installed in the Rated home (the denominator). By default, this means that the equipment and fuel types for the Reference Home must be the same as that of the Rated Home. This equipment efficiency ratio is then multiplied by the respective loads for the Rated home to arrive at its Modified Loads. This procedure is performed successively for the heating, cooling and hot water loads of the Rated Home. The individual Modified Loads for the Rated Home are then added together and compared with the summation of the actual loads for the Reference Home. The results of these calculations are used to "score" the relative energy-efficiency of the building and its related equipment with respect to the national minimum standards. Table B provides an example.
Table B. Example of Modified Loads
Method Calculation
using Equipment Efficiency Ratios
| End Uses | Reference Home |
Rated Home |
||||
Load (MBtu) |
Eq. Eff. |
Load (MBtu) |
Eq. Eff. |
EqEf Ratio |
Mod Load (MBtu) |
|
| Heating | 40.0 |
0.78 |
38.0 |
0.80 |
0.975 |
37.1 |
| Cooling(1) | 30.0 |
2.93 |
32.0 |
2.93 |
1.000 |
32.0 |
| Hot Water | 20.0 |
0.54 |
20.0 |
0.60 |
0.900 |
18.0 |
TOTALS |
90.0 |
87.1 |
||||
(1) Eq. Eff. for vapor compression
equipment = Mfg. Rating / 3.413 |
||||||
However, Guideline #12 of the HERS Council Guidelines does not use equipment efficiency ratios as the means to arrive at Modified Loads instead it uses end-use energy consumption ratios (called e-Ratios here). At first glance, this may seem contradictory to the preceding discussion. However, there is no contradiction because equipment efficiency and energy consumption are proportionally related, albeit inversely, through Eq. 2. If the example given in Table B is recast in terms of energy consumption, the consistency between the two procedures can be illustrated.
Table C. Example of Modified Loads
Method Calculation
using Energy Ratios (e-Ratio)
| End Uses | Reference Home |
Rated Home |
||||||
Load (MBtu) |
Eq. Eff. |
Energy (MBtu) |
Load (MBtu) |
Eq. Eff. |
Energy (MBtu) |
e-Ratio |
Mod Load (MBtu) |
|
| Heating | 40 |
0.78 |
51.3 |
38 |
0.80 |
47.5 |
0.926 |
37.1 |
| Cooling | 30 |
2.93 |
10.2 |
32 |
2.93 |
10.9 |
1.067 |
32.0 |
| Hot Water | 20 |
0.54 |
37.0 |
20 |
0.60 |
33.3 |
0.900 |
18.0 |
| TOTALS | 90 |
87.1 |
||||||
Although derived using a slightly different procedure, the Modified Loads and Point Score given in Table C are identical to those of Table B. The differences between the two tables are purely procedural rather than substantive. In Table B the EqEf Ratio is constructed using the Reference Home equipment efficiency as the numerator and Rated Home equipment efficiency as the denominator. In Table C the e-Ratio is derived using the Rated Home energy consumption as the numerator and the Reference Home energy consumption as the denominator. Thus, in Table B the Modified Loads are determined by multiplying the EqEf Ratio by the Rated Home loads and in Table C the Modified Loads are determined by multiplying the e-Ratio by the Reference Home loads. This procedural difference is necessitated by the fact that energy use and equipment efficiency ratings are inversely proportional (see Eq. 2).
There are good and valid reasons for constructing Modified Loads using the procedures illustrated in Table C rather than those used for Table B. If the procedures of Table B are used to construct Modified Loads, then only simplified, seasonal equipment efficiency ratings can be used to construct scores. On the other hand, the procedures illustrated by Table C allow hourly, climate-specific evaluation of equipment performance to be fully considered in the equipment performance analysis without losing the ability to also derive scores based on the more simplified, seasonal equipment performance ratings commonly used in today's marketplace. This is an important distinction that allows the rating method to more fully accommodate the future, when both equipment innovations and improved equipment simulation capabilities are expected in the marketplace.
The revised equations for calculating the point score require a 2-step process, starting by calculating the Modified End Use Load for heating, cooling and hot water separately as follows:
| MEUL = REUL * (EC_x / EC_r) | Eq. 3 |
|||
| where: | ||||
| MEUL = | Modified end use load (for heating, cooling and water heating). | |||
| REUL = | Reference Home end use load (for heating, cooling and water heating). | |||
| EC_x = | Rated Home's estimated energy consumption (for heating, cooling and water heating). | |||
| EC_r = | Reference Home's estimated energy consumption (for heating, cooling and water heating). | |||
Equation 3 states that the modified end use loads (for the Rated home) are equal to the Reference Home end use loads multiplied by the ratio of the estimated energy uses (which are a derivative of the equipment performance efficiencies) of the two homes.
Step 2 involves adding the three loads together for both the Reference Home and the Rated Home and calculating the point score as follows:
| Point score = 100 - 20 * (TML / TRL) | Eq. 4 |
|||
| where: | ||||
| TML = | MEUL_heating + MEUL_cooling + MEUL_hot water (Total of all Rated Home's modified end use loads as calculated using equation 1). | |||
| TRL = | REUL_heating + REUL_cooling + REUL_hot water (Total of all Reference Home's actual end use loads). | |||
Thus, the denominator of the rating fraction (TML / TRL) now contains the sum of the building loads for the Reference Home, which do not change as a function of fuel type. As a result, the reference for the point score can no longer "float" with fuel type, even though the fuel type for the Reference Home is still required to be the same as in the Rated Home. In addition, since rating is accomplished with building loads rather than energy consumption, envelope efficiency features are appropriately "weighted" with respect to the overall building efficiency.
Although the Modified Loads Method solved very important problems, it still contains a perceived fuel neutrality flaw. The problem is that different fuel types may be discriminated against in the marketplace for purely technological reasons that are largely beyond the control of the fuel industry. The problem is simple enough the available market potential for improvement of equipment efficiencies beyond the NAECA minimum standards is not equal across fuel types. This problem is illustrated in Table D below using a simple, space heating example. The EEC columns given in the Table are Equipment Efficiency Coefficients (the energy use per unit load expressed in like units as the load [e.g. Btu/Btu]) for the natural gas (EEC_g) and electric heating systems (EEC_e), respectively.
Table D. Gas versus electric energy improvement potentials.
| Space Heating | Natural Gas |
Electric |
||
AFUE |
EEC_g |
HSPF |
ECC_e |
|
| NAECA Standard | 0.78 |
1.2821 |
6.8 |
0.5019 |
| Best Technology | 0.96 |
1.0417 |
10 |
0.3413 |
%Change |
-18.7% |
-32.0% |
||
Thus, all other things being equal, the space heating energy use in an electrically heated home may be improved (decreased) by 32% by upgrading from the reference standard (NAECA) equipment to the best available market technology equipment. However, space heating energy use can be improved (decreased) by only 18.7% if the home is heated by a natural gas-fired furnace. The ratio of these two energy end use improvement potentials (electric with respect to natural gas) is 1.7 to 1.
The Normalized Modified Loads Method
In June 1998, NASEO and RESNET began a process designed to reach a consensus on a set of national Technical Guidelines for home energy ratings. DOE's failure in 1996 to promulgate a federal Rule on the subject had restricted the market for home energy ratings and the state energy officials and the rating industry hoped to provide the set of nationally acceptable standards that DOE did not publish. This process resulted in the development and publication of the Normalized Modified Loads Method of rating home energy efficiency.
It is mathematically possible to "normalize" Modified End Use Loads to reflect differences in equipment improvement potentials such that all equipment improvements are normalized with respect to the improvement potential of a "baseline" fuel type. This normalized Modified End Use Load (nMEUL) will then provide equal changes in HERS Scores across fuel types, all other things being equal. To accomplish this it is necessary to select a "baseline" improvement potential and then scale the energy improvement potentials for other fuel types to that of the "baseline." For this purpose, the improvement potential of electric equipment is selected as the "baseline."
It is critical that Equation 3 maintain its general form, consisting of Reference Home End Use Loads modified by the ratio of the estimated energy consumption of the Rated and Reference Homes' end use Energy Consumptions. This is necessary to allow detailed mechanical system modeling to be used in the simulation of the two homes. Otherwise, it will not be possible to accurately represent the impacts that local climates will have on equipment performance and energy consumption. Thus, Equation 3 should not directly contain any simplified, manufacturers' equipment performance rating values like AFUE or HSPF.
Thus, the form of the revised Equation 3 remains the same as the original equation, as follows:
| nMEUL = REUL * (nEC_x / EC_r) | Eq. 5 |
|||
| where: | ||||
| nMEUL = | the normalized Modified End Use Loads (for heating, cooling and water heating) | |||
| nEC_x = | the normalized Energy Consumption for the Rated Home load (for heating, cooling and water heating) | |||
| EC_r = | the Energy Consumption for the Reference Home load (for heating, cooling and water heating) | |||
The remaining task is the determination of nEC_x, the normalized energy consumption for the Rated Home's end use loads.
Derivation of nEC_x
For the purposes of this derivation, the general equation for each end-use energy consumption is defined as follows:
| EC = EEC * EUL | Eq. 6 |
|||
| where: | ||||
| EC = | Energy Consumption (Btu-input) | |||
| EEC = | Equipment Efficiency Coefficient (Btu-input/Btu-output) | |||
| EUL = | End Use Load (i.e. the amount of heat that must be added or removed to satisfy a thermostat) (Btu-output) | |||
More specific forms of the Equation 6 variables that specify fuel type and equipment efficiency coefficient are written using subscripts with the following general formats:
EC_u,v = EC using fuel type "u" and equipment efficiency coefficient "v"
EEC_u,v = EEC using fuel type "u" and equipment efficiency coefficient "v"
At this point, it is critically important to note that the EUL term in Equation 6 is independent of both fuel type and equipment efficiency. This is the required critical premise of all modified load rating methods.
The following subscripts are used in the development of this derivation to signify fuel type and equipment efficiency coefficient:
| o = | the "other" fuel type (i.e. other than the "baseline" fuel type) |
| e = | the "baseline" fuel type (taken to be electric power) |
| x = | the given equipment (i.e. the equipment of the "Rated" home) |
| r = | the reference equipment (taken to be the NAECA minimum standard ) |
| b = | the best available market equipment (taken from the ARI and GAMA guides) |
The end use loads for the Reference Home do not change as a function of fuel type (i.e. by definition, EUL_e,r = EUL_o,r) and the "rating fraction" used in Eq. 4 to determine the Point Score consists of the ratio of the Total Modified Loads with respect to the Total Reference Loads (i.e. MEUL / REUL). Therefore, for the Point Score to be the same for the case where the relative change in efficiency potential (i.e. EEC) is the same for both the "baseline" and some "other" fuel type, the Modified End Use Loads also must be equal (i.e. MEUL_e,x = MEUL_o,x). However, this will not be the case, and MEUL_o,x must be normalized in some way, such that its modified value equals MEUL_e,x (i.e. such that nMEUL_o,x = MEUL_e,x).
The equation that expresses the point at which the EEC change potential is equal between the "baseline" and the "other" fuel type is as follows:
(EEC_e,r - EEC_e,x) |
(EEC_o,r - EEC_o,x) |
|||
--------------------- |
= |
--------------------- |
Eq. 7 |
|
(EEC_e,r - EEC_e,b) |
(EEC_o,r - EEC_o,b) |
Rearranging Equation 7 to solve for EEC_e,x (the "baseline" equivalent of EEC_o,x), one obtains:
(EEC_o,r - EEC_o,x) |
||||||
EEC_e,x = EEC_e,r |
- |
-------------------- |
* |
(EEC_e,r - EEC_e,b) |
Eq. 7a |
|
(EEC_o,r - EEC_o,b) |
However, to "normalize" Eq. 7a such that it may be used as a "normalization factor" to modify the EEC of "other" fuel types, it is necessary to divide both sides of the equation by the "baseline" fuel type's reference standard (EEC_e,r). In other words:
| nEEC_o,x = (EEC_e,x / EEC_e,r ) | Eq. 8 |
|||
Substituting Eq. 7a into Eq. 8 yields the following normalization equation:
(EEC_o,r - EEC_o,x) |
(EEC_e,r - EEC_e,b) |
|||||
nEEC_o,x = 1 |
- |
--------------------- |
* |
--------------------- |
Eq. 9 |
|
(EEC_o,r - EEC_o,b) |
EEC_e,r |
At this point ´nEEC_o,x' represents the "normalization factor" by which the given equipment efficiency coefficient for any "other" fuel type (EEC_o,x) may be modified to produce the same relative change in EEC (with respect to its potential to change) as is produced by the change in the "baseline" fuel type.
And on rearranging the right-hand side of Eq. 9 to isolate EEC_o,x (the only variable that can not be known a priori), one obtains:
(EEC_e,r - EEC_e,b) |
||||||
nEEC_o,x |
= |
-------------------------------- |
* |
EEC_o,x |
||
(EEC_o,r - EEC_o,b)
* EEC_e,r |
||||||
EEC_o,r * (EEC_e,r
- EEC_e,b) |
||||||
- |
-------------------------------- |
+ |
1 | Eq. 9a |
||
EEC_e,r * (EEC_o,r
- EEC_o,b) |
Now Eq. 9a may be re-written in a simple and desirable ´y = a*x + b' format as follows:
| nEEC_o,x = a * EEC_o,x + b | Eq. 10 |
|||
| where: | ||||
| a = | (EEC_e,r - EEC_e,b) / [(EEC_o,r - EEC_o,b) * EEC_e,r] | Eq. 11 |
||
| b = | [EEC_o,r * (EEC_e,r - EEC_e,b)] / [EEC_e,r * (EEC_o,r - EEC_o,b)] - 1 |
Eq. 12 |
||
Checking the limiting case, where the "baseline" equipment type is substituted for the "other" equipment type (i.e. EEC_o = EEC_e), coefficient ´a' evaluates as 1 / EEC_e,r and coefficient ´b' evaluates as 0. From Equation 10 for this case, nEEC_e,x = EEC_e,x / EEC_e,r, as should be the case.
Given Equations 11 and 12 and a table of values for EEC, it is possible to construct a table of ´a' and ´b' coefficients for Eq. 10. Table E below provides EEC values derived from the Manufacturer's Equipment Performance Ratings (MEPR) given by the ARI (American Refrigeration Institute) Guide8 and the GAMA (Gas Appliance Manufacturers Association) Guide.9 From Equation 6, EEC is the unitless Equipment Efficiency Coefficient, which when multiplied by EUL (End Use Load) yields EC (Energy Consumption) in like units as EUL. However, the MEPR values given in the above Guides are constructed either as the reciprocal of EEC (for gas equipment) or as the reciprocal of EEC multiplied by the Btu/watt conversion factor of 3.413 (for electric equipment). Therefore, it is necessary to modify MEPR accordingly to yield the EEC values given in Table E below.
Table E. Manufacturer's Equipment Performance
Ratings (MEPR) and
Equipment Efficiency Coefficients (EEC) for the NAECA reference
standard (´r') and the best available market technology equipment
(´b').
| Rated Home Fuel Type and End Use |
Reference Home NAECA Standard |
Best Available Market Technology |
||
MEPR_r |
EEC_r |
MEPR_b |
EEC_b |
|
| Electric Space Heating(1) | HSPF = 6.8 |
0.5019 |
HSPF = 9.85 |
0.3465 |
| Natural Gas Space Heating (2) | AFUE = 0.78 |
1.2821 |
AFUE = 0.966 |
1.0352 |
| Fuel Oil Space Heating (2) | AFUE = 0.78 |
1.2821 |
AFUE = 0.866 |
1.1547 |
| Any Type Space Cooling (1) | SEER = 10.0 |
0.3413 |
SEER = 17.0 |
0.2008 |
| Electric Water Heating (1) | EF = 0.88 |
1.1364 |
EF = 2.50 |
0.4000 |
| Natural Gas Water Heating (2) | EF = 0.54 |
1.8519 |
EF = 0.86 |
1.2628 |
| Fuel Oil Water Heating (2) | EF = 0.53 |
1.8868 |
EF = 0.68 |
1.4706 |
(1) Taken from the ARI Guide (see footnote 8) |
||||
On substituting the EEC_r and EEC_b values given in Table E into Equations 11 and 12, the values for Eq. 10 coefficients ´a' and ´b' in are produced, as follows:
Table F. Coefficients used to determine
nEC_x for a given fuel type and end use.
| Rated Home Fuel Type and End Use |
'a' |
'b' |
| Electric Space Heating | 1.9924 |
0 |
| Natural Gas Space Heating | 1.2544 |
0.6082 |
| Fuel Oil Space Heating | 2.4321 |
2.1180 |
| Electric Air Conditioning | 2.9301 |
0 |
| Electric Water Heating | 0.8800 |
0 |
| Natural Gas Water Heating | 0.9404 |
0.7415 |
| Fuel Oil Water Heating | 1.5569 |
1.9376 |
From Eq. 6, one knows that EUL = EC / EEC. In order to "normalize" the end use load so that it is independent of fuel type, EEC must be modified using the normalization factor derived in Eq. 10. From this relationship, one can define an additional equation for nMEUL, as follows:
| nMEUL = EC_x / (EEC_x / nEEC_x) | Eq. 13 |
|||
Recalling that the left-hand sides of Eq. 5 and Eq. 13 are equal, one may set their right-hand sides equal and write:
| REUL * (nEC_x / EC_r) = EC_x / (EEC_x / nEEC_x) | Eq. 14 |
|||
And substituting Eq. 10 into Eq. 14 and rearranging, one obtains the final form of the equation to determine nEC_x, as follows:
| nEC_x = (a * EEC_x - b) * (EC_x * EC_r) / (EEC_x * REUL) | Eq. 15 |
|||
| where: | ||||
| nEC_x = | the normalized Energy Consumption for the Rated Homes's end uses computed separately for heating, cooling and hot water. | |||
| EEC_x = | the Equipment Efficiency Coefficient for the Rated Home's end use as derived from the manufacturer's equipment performance rating (MEPR) as either 1.0 / MEPR or 3.413 / MEPR, whichever is appropriate. | |||
| EC_x = | the Energy Consumption for the Rated Home's end uses as computed using accredited simulation tools. | |||
| EC_r = | the Energy Consumption for the Reference Home's end uses as computed using accredited simulation tools. | |||
| REUL = | the Reference Home's End Use Loads as computed using accredited simulation tools. | |||
However, Section B.4.a.(17) of the Technical Guidelines requires that the Manufacturer's Equipment Performance Rating for the Reference Home be modified by a Distribution System Efficiency (DSE_r) of 0.80 for all heating and cooling systems. To account for this requirement, it is necessary to modify the EC_r value in Eq. 15 by DSE_r as follows:
| nEC_x = (a * EEC_x - b) * (EC_x * EC_r * DSE_r) / (EEC_x * REUL) | Eq. 16 |
|||
| where: | ||||
| DSE_r = | REUL/EC_r * EEC_r | |||
For simplified system performance methods, DSE_r equals 0.80 for heating and cooling systems and 1.00 for hot water systems.10 However, for detailed modeling of heating and cooling systems, DSE_r may be less than 0.80 as a result of part load performance degradation, coil air flow degradation, and auxiliary resistance heating for heat pumps. It is important to note that if detailed systems modeling is employed, it must be applied equally to both the Reference and the Rated Homes. Thus, in its final form, Eq. 16 may be reduced to:
| nEC_x = EC_x * (a * EEC_x - b) * (EEC_r / EEC_x ) | Eq. 17 |
|||
At this point nEC_x has been determined in a form suitable for use in the general equations used to determine point score and the normalized Modified End Use Loads (nMEUL) for the Rated Home may be calculated using Eq. 5 as follows:
| nMEUL = REUL * (nEC_x / EC_r) | ||||
| where: | ||||
| nMEUL = | the Rated Home's normalized Modified End Use Loads computed separately for heating, cooling and hot water. | |||
And the Point Score is then computed using Eq. 4, as follows:
| Point Score = 100 - 20 * (TnML / TRL) | ||||
| where: | ||||
| TnML = | the Total of the Rated Home's normalized Modified Loads for heating, cooling and hot water. | |||
| TRL = | the Total of the Reference Home's Loads for heating, cooling and hot water. | |||
Conclusions
On September 19, 1999, at its annual meeting in Indianapolis, Indiana, the Board of Directors of the National Association of State Energy Officials (NASEO), adopted the National Home Energy Rating Technical Guidelines. These NASEO Guidelines incorporate the Normalized Modified Loads Method of rating. Notwithstanding the fact that these Technical Guidelines were adopted by unanimous vote of the NASEO Board, considerable contention over the rating method still remains within the fuels industry. The electric industry, represented by the Edison Electric Institute (EEI), and the natural gas industry, represented by the American Gas Association (AGA), remain at odds with one another over the adopted rating method.
EEI has stated publically that its constituency can accept only the modified loads method. It is fundamentally opposed to the basic premise of the normalized modified loads method and believes that "handicapping" based on the market potential of fuel types to achieve energy savings grossly misrepresents the actual site energy savings that can be achieved by gas-fueled equipment. On the other hand, AGA has stated publically that its constituency can accept only rating methods that use source energy accounting methods to compare electric and gas fuels directly against one another. There has been no evidence presented by either EEI or AGA indicating that some type of compromise between these two positions could ever be achieved.
Acknowledgments
Countless individuals have been involved in the long and arduous process summarized by this paper. Each and every one of them has contributed to the effort to reach a fair and equitable solution to the fuel neutrality issue. It is not possible to list each contributor, but the process would have surely floundered long ago except for the leadership of the executive directors of the primary organizations that have taken on this challenge. Ms. Cynthia Gardstein of the HERS Council, Mr. Steve Baden of RESNET and Mr. Frank Bishop of NASEO deserve much gratitude for their faithful and selfless service as the guardians of this process. The authors also wish to thank Dr. M.V. Swami of the Florida Solar Energy Center and Mr. Henry Spindler of Conservation Services Group for their assistance in the derivation of the normalization procedures that are used in the Normalized Modified Loads Method.
- In addition to this succession, the California Energy Commission
has adopted a regulation that requires energy ratings in California
to be "scored" using source energy consumption. To
date, no specific method of accomplishing this has been formally
proposed by California and, therefore, this to-be-determined
method is not discussed in this paper.
- Guideline #12, Guidelines for Uniformity:
Voluntary Procedures for Home Energy Ratings, Version 1, July 1995,
Home Energy Rating Systems (HERS) Council, Washington, DC.
- "Voluntary Home Energy Rating
Guidelines." Federal Register, Tuesday, July 25, 1995.
Vol. 60, No. 142, pp. 37949-37966. U.S. Government Printing
Office, Washington, DC.
- Fairey, P., April 11, 1996. "A
Comparative Analysis of Present and Proposed Rating Methods for
Computing HERS Scores (Revised)," HERS
Council Technical Committee Research Report No. FSEC-RR-41-98,
Florida Solar Energy Center, Cocoa, FL.
- "Voluntary Home Energy
Rating Guidelines." Federal Register, Tuesday, April 9,
1996, Vol. 61, No. 69, pp 15736-15738. U.S. Government Printing
Office, Washington, DC.
- Guideline #12, Guidelines for Uniformity:
Voluntary Procedures for Home Energy Ratings, Version 2.0, August
1996. Home Energy Rating Systems (HERS) Council, Washington, DC.
- Personal Communication with Dick
Tracey and John Reese, who at that time were drafting the final
DOE Rule.
- ARI Electronic Unitary Directory, "ARI
Standard Ratings for Unitary Air-Source Heat Pumps," January
1, 1999 - June 30, 1999. American Refrigeration Institute.
- Consumers' Directory of Certified
Efficiency Ratings for Residential Heating and Water Heating
Equipment, October 1998 - April 1999. Gas Appliance Manufacturers
Association.
- Section B.4.a.(17), National Home Energy Rating Technical Guidelines, September 19, 1999. National Association of State Energy Officials, Washington, DC.
