
Reference Publication: Fairey, P., "An Analysis of Greenhouse Cookpot Design Considerations For Low-Cost Solar Cookers." Contract Report FSEC-CR-1283-01, Florida Solar Energy Center, Cocoa, FL, October 29, 2001. Disclaimer: The views and opinions expressed in this article are solely those of the authors and are not intended to represent the views and opinions of the Florida Solar Energy Center. |
An
Analysis of Greenhouse Cookpot Design
Considerations For Low-Cost Solar
Cookers
Philip
Fairey
Florida
Solar Energy Center (FSEC)
FSEC-CR-1283-01
Background
This analysis is prepared as part of a research project on low-cost solar cookers conducted by the Florida Solar Energy Center for the Dorothy Ann Foundation on behalf of Solar Household Energy, Inc. The overall purpose of the research project is to improve the performance, reliability and cost-effectiveness of low-cost solar cookers for use in developing nations. The analysis reported here concentrates solely on the cookpot and "greenhouse" design considerations for such systems.
Purpose
The purpose of the analysis is to examine the thermal design parameters for greenhouse cookpots used in low-cost solar cookers. The analysis concentrates on methods of conserving collected solar radiation so that it is applied to the primary task of cooking food. This is an important consideration in virtually all solar thermal systems because outdoor exposure (and the consequential heat loss of this exposure) is a necessary design consideration of such systems, especially in low-cost solar cookers.
There are a large variety of solar cookers. Most attempt to concentrate the available solar energy onto the cooking vessel through the use of "reflectors." Previous analysis have studied the effectiveness of both faceted and curved reflectors. This analysis examines the thermal considerations for "greenhouse" cookpots whereby the cooking vessel is integral to the transparent "cover" of the cooking system. This is accomplished by "nesting" a solar absorbing cooking vessel (cookpot) inside a slightly larger transparent vessel (greenhouse) of the same shape. A number of thermal engineering design parameters are studied through an analysis designed to determine the relative impact of each. The following questions summarize the intent of the analysis.
- What is the importance of the tightness of the seal between the cookpot and the transparent greenhouse cover?
- What is the importance of the far-infrared surface emittance properties of the cookpot and the greenhouse cover?
- What is the importance of the convective heat transfer rate between the cookpot and the greenhouse cover?
The analysis makes no attempt to study the cookpot and greenhouse lid. Neither the lid heat transfer mechanisms nor the seal between the lid and the cookpot and greenhouse are studied by this analysis. Rather the simplifying assumption is made that thermal energy losses at the cookpot lid are exactly balanced by its solar energy gains.
Methods
The analysis is conducted using classical steady-state heat transfer theory. The problem is constituted as a series of temperatures (nodes) which interact with one another through heat transfer mechanisms (conduction, convection and radiation) with given temperatures at the two ends (boundary conditions) of the series of nodes. For each node in the system, an energy balance equation is written to conserve energy. The resulting system of equations is then solved to determine the "unknown" values. Figure 1 below shows a schematic diagram of the greenhouse cookpot configuration that is analyzed.
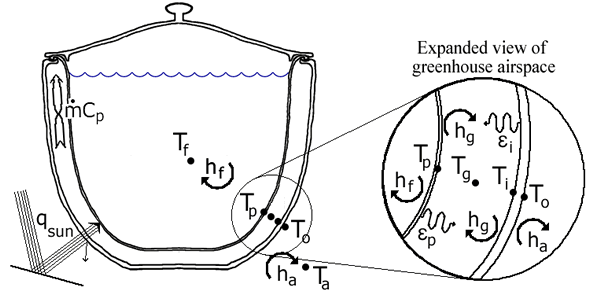 |
| Figure 1. Schematic diagram showing heat transfer mechanisms considered by the greenhouse cookpot analysis. |
The given boundary conditions for the problem are the temperature of the fluid in the cookpot (Tf) and the temperature of the ambient (outdoor) air (Ta), such that Tf = 212 oF and Ta = 80 oF. It is important to point out that the cookpot fluid is assumed not to boil so that there is no mass loss from the system. The inputs to the system of equations consist of the heat transfer coefficients (hx) at the 4 cookpot and greenhouse surfaces, the surface emittances (ex) of the 2 greenhouse surfaces, the mass capacitance flow rate (mCp) of the ambient air passing through the greenhouse, the solar absorptances (Ax) of the greenhouse glass and cookpot surfaces and the transmissivity (tg) and thermal resistance (Rg) of the greenhouse glass.
The unknowns for the system of equations are the temperatures of the greenhouse glass surfaces (To and Ti), the greenhouse air temperature (Tg), and the cookpot surface temperature (Tp) and the reflected solar radiation (qsun) required to maintain the cookpot fluid temperature at 212 oF. Thus, there are a total of 5 unknowns. This requires that there be a system of 5 energy balance equations in order to achieve a solution.
Steady-state energy balance equations
The system of energy balance equations (given at the temperature nodes) for the problem are as follows:
@ To: -qsun*Ag + ha(To-Ta) + 1/Rg(To -Ti) = 0
@ Ti: 1/Rg(Ti-To) + hg(Ti-Tg) + E(Ti4-Tp4) = 0
@ Tg: hg(Tg-Ti) + hg(Tg-Tp) + mCp(Tg-Ta) = 0
@ Tp: -qsun * tg * Ap + hf(Tp-Tf) + hg(Tp-Tg) + E(Tp4-Ti4) = 0
@ Tf: hf(Tf-Tp) = 0
where:
qsun = solar flux reflected onto greenhouse
A = solar absorptance at node (see subscripts)
h = convection coefficient at node (see subscripts)
T = temperature at node (see subscripts)
mCp = mass capacitance flow rate for infiltration air
Rg = thermal resistance of greenhouse glass
tg = solar transmissivity of greenhouse glass
E = effective greenhouse cavity emissivitywhere:
E = 1.713*10-9/(1/ei + 1/ep - 1)
e = surface emittance of node (see subscripts)and where the subscripts indicate:
a = ambient
o = outside glass surface
i = inside glass surface
g = greenhouse/glass
p = pot surface
f = fluid in pot
A small computer program was created to solve the above system of steady-state energy balance equations using the Newton method matrix solution technique.
The solution output of greatest interest is qsun, the amount of reflected solar radiation needed to keep the cookpot fluid at 212 oF. The smaller this value, the more effective the greenhouse cookpot and the simpler the required reflector design.
To examine the range of reasonable greenhouse cookpot design configurations, the following set of simulation cases are generally described:
Base case: This is the reference case with no improvements. The cookpot is simply rested on the lip of the greenhouse glass container with no seal, standard glass is used for the greenhouse container and the cookpot surface is standard black paint.
Sealed greenhouse: The same as the base case except that the joint between the greenhouse container and the cookpot is sealed against air leakage.
Solar glass: The same as the sealed case except that the greenhouse container is made from low-iron, high-transmissivity glass.
Low-e coatings: The same as the solar glass case except that the cookpot surface and the inside of the greenhouse container have low-emittance surface coatings.
Evacuated greenhouse: The same as the solar glass case except that the air is evacuated from the greenhouse air space.
Dewar greenhouse: The same as the evacuated case except that the cookpot and the inside surface of the greenhouse container have low-emittance surface coatings.
It is also necessary to establish a set of simulation inputs for these cases. Table A below gives the units and values for each input variable for each of the simulated cases. Differences from the base case are highlighted.
Table A. Input for Greenhouse Cookpot Analysis Simulation Cases
Input Variable |
Simulation Case |
||||||
Symbol |
Units |
Base |
Sealed |
Solar glass |
Low-e |
Evacuated |
Dewar |
ha |
Btu/h-ft2-oF |
4.0 |
4.0 |
4.0 |
4.0 |
4.0 |
4.0 |
Ag |
unitless |
0.08 |
0.08 |
0.05 |
0.10 |
0.05 |
0.10 |
tg |
unitless |
0.86 |
0.86 |
0.90 |
0.85 |
0.90 |
0.85 |
Rg |
h-ft2-oF/Btu |
0.15 |
0.15 |
0.15 |
0.15 |
0.15 |
0.15 |
ei |
unitless |
0.86 |
0.86 |
0.86 |
0.15 |
0.86 |
0.15 |
hg |
Btu/h-ft2-oF |
0.68 |
0.68 |
0.68 |
0.68 |
0 |
0 |
mCp |
Btu/h-ft2-oF |
0.044 |
0 |
0 |
0 |
0 |
0 |
Ap |
unitless |
0.90 |
0.90 |
0.90 |
0.85 |
0.90 |
0.85 |
ep |
unitless |
0.90 |
0.90 |
0.90 |
0.15 |
0.90 |
0.15 |
hf |
Btu/h-ft2-oF |
580 |
580 |
580 |
580 |
580 |
580 |
The ASHRAE Handbook of Fundamentals is the reference source for the majority of the input values, however, the mass capacitance flow rate (mCp) and the pot fluid convection coefficient (hp) are determined through "educated engineering estimate" methods. Calculation of the cookpot fluid convection coefficient (hp) is the simpler to estimate. It is expected to be quite large as water is a fluid of great density as compared with air. It is also expected to have only a minor impact on the outcome of the analysis because it is not varied from case to case and its function is to keep the cookpot surface temperature very close to the temperature of the cookpot fluid in order not to prejudice the analysis away from the desired objective of better defining the thermal impacts of the greenhouse design. For simplicity sake this value is set equal to the still air film coefficient for air (0.68) multiplied by the density ratio of water to air (850) or 580 Btu/h-ft2-oF.
The mass capacitance flow rate (mCp) is more difficult. It requires definition of a greenhouse cookpot geometry and an assumption regarding the rate of air exchange between the greenhouse airspace and ambient. The geometry of the cookpot shown in Figure 1 was approximated to consist of a hemisphere (cookpot bottom) toped by a cylinder of equal radius with a height equal to 15% of that radius. With these assumptions, the radius of the hemisphere and cylinder were calculated as 4.92" (12.5 cm), so as to give a cookpot volume of 5 liters (the design requirement for the solar cooker being investigated). The greenhouse container geometry was then established to provide a 0.5" (1.27 cm) airspace between the greenhouse container and the cookpot surface and it's volume calculated (6.685 liters). The volume of the cookpot was then subtracted from the volume of the greenhouse container to give the volume of the air contained within the greenhouse airspace of 1.685 liters or 0.06 ft3 (103 in3).
The density of air at standard temperature and pressure is 0.075 lb/ft3 and its heat capacity is 0.20 Btu/lb-oF. Multiplying these values together with the volume of the greenhouse airspace gives the thermal mass capacity for the air in the greenhouse airspace of 8.93 x 10-4 Btu/oF. The surface area of the cookpot, however, is not unity so this value must be normalized by dividing it by the cookpot surface area of 1.213 ft2 to yield an area-normalized thermal mass capacitance of 7.36 x 10-4 Btu/ft2-oF for the greenhouse airspace.
Next, it is necessary to assume some air exchange rate between the greenhouse airspace and the outdoors (ambient). To our knowledge, there are no research data indicating reasonable ranges for this value and a relatively large value of 1.0 air exchange per minute (60 air exchanges per hour) was assumed. Multiplying the area-normalized mass capacitance of the greenhouse air by this air exchange rate gives the final mass capacitance flow rate of 0.044 Btu/h-ft2-oF that is used in the simulations.
Results
The analyses were completed using the previously described Newton method solution technique. Results clearly indicate that certain attributes are significantly more important than others. For example, even though one might think that the seal between the greenhouse and the cookpot would be of paramount importance, the simulations show that this attribute has only a small impact when compared with the base case, which is assumed to be unsealed.
Table B presents the results of the analysis. As previously stated, qsun, the amount of reflected solar radiation needed to keep the cookpot fluid at 212 oF, is the parameter of greatest interest. The smaller this value, the more effective the greenhouse cookpot and the simpler the required reflector design. Table B below shows that this value ranges from a high of 148 Btu/h-ft2 for the base case to a low of 34 Btu/h-ft2 for the Dewar (Thermos bottle) case. We can also see from the results that surface emittance plays a large role in overall efficiency, with the Low-e case requiring only 41% the solar input as the base case.
Table B. Output for Greenhouse Cookpot Analysis Simulation Cases
Output Variable |
Simulation Case |
||||||
Symbol |
Units |
Base |
Sealed |
Solar glass |
Low-e |
Evacuated |
Dewar |
To |
oF |
130.77 |
130.99 |
130.11 |
112.58 |
126.19 |
106.98 |
Ti |
oF |
147.45 |
147.84 |
147.13 |
119.22 |
140.98 |
110.65 |
Tg |
oF |
177.23 |
179.92 |
179.56 |
165.61 |
150.99 |
140.88 |
Tp |
oF |
212.00 |
212.00 |
212.00 |
212.00 |
212.00 |
212.00 |
qsun |
Btu/h-ft2 |
148 |
145 |
140 |
61 |
122 |
34 |
% of Base Case: |
100% |
98% |
95% |
41% |
82% |
23% |
|
Conclusions
It is clear from the findings of this analysis that the greenhouse cookpot design for solar cookers can have overwhelming impacts on performance. There is more than a factor of 4 difference between the amount of solar radiation needed to keep the base case cookpot at 212 oF and the amount needed to keep the Dewar greenhouse cookpot at that temperature. In effect, this means that the base case greenhouse cookpot configuration would need a solar radiation concentration ratio of more than 4 to equal the performance of the Dewar greenhouse cookpot configuration with a solar concentration ratio of unity.
Acknowledgments
The author is very grateful to Muthusamy Swami and Safvat Kalaghchy for their assistance in formulating and computerizing the mathematical solver that was used to perform these simulations.
